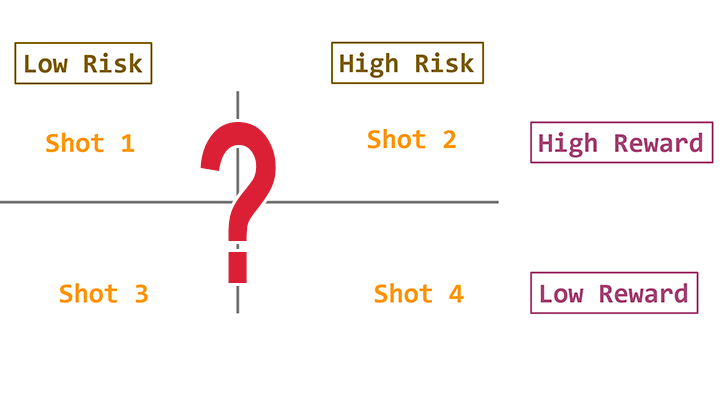
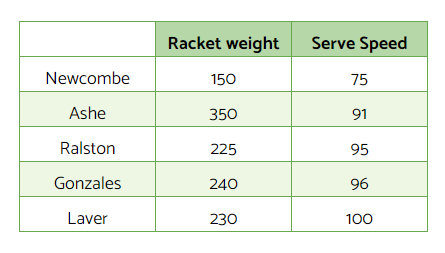
Can you serve 100mph? If you can you are way better than me! 100mph was a great serve in the 1960s and 1970s. The book “Fundamentals of Tennis” (Pagenhoef 1970) lists serving speeds vs racket weight for numerous top players who were using wooden rackets. Only one player was regularly serving 100mph. Rod Laver.
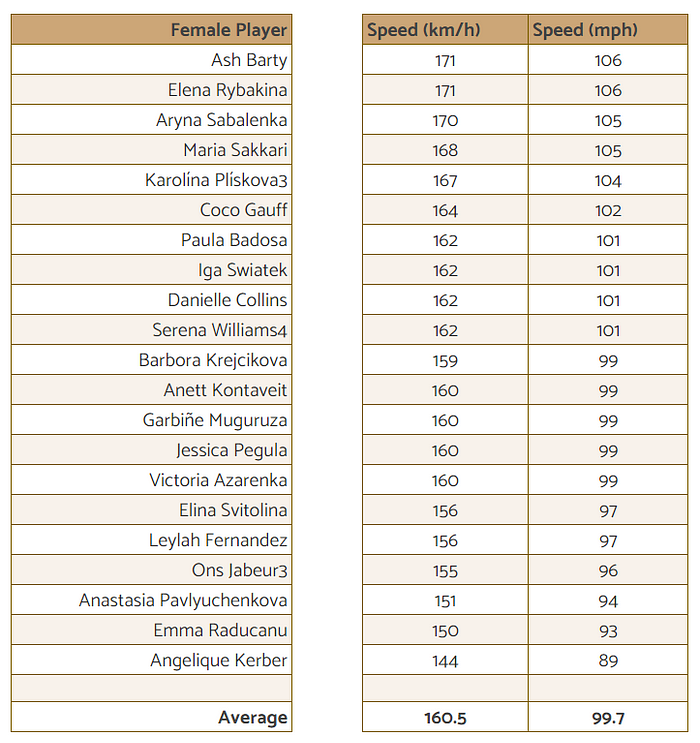
Even today, 100mph is a strong serve. In fact, in the professional women’s game, it is a top 10 in the world serve! As it happens 100mph is currently exactly the average 1st serve speed of the WTA top 20.
Now simply hitting the ball over the net at 100mph is tough, but what is incredible is how does the ball go in the court?!
If you simply plug 2.7m height (the typical height of the ball from ground on serving in WTA) into a triangle calculator, then to clear the net height of 0.91m (a fall of 1.79m) at 11.88m from baseline; then a downward angle of -8.5deg would be needed. The triangulation suggests that this ball would just go in by 20cm. However try serving like that and it does not work. Not even close. You actually need an angle of -5.3deg (optimal serving angle) but wait in the triangle calculator: it seems like with a -5.3deg 100mph ball would hit the ground after 29m….or 5m beyond the baseline!!
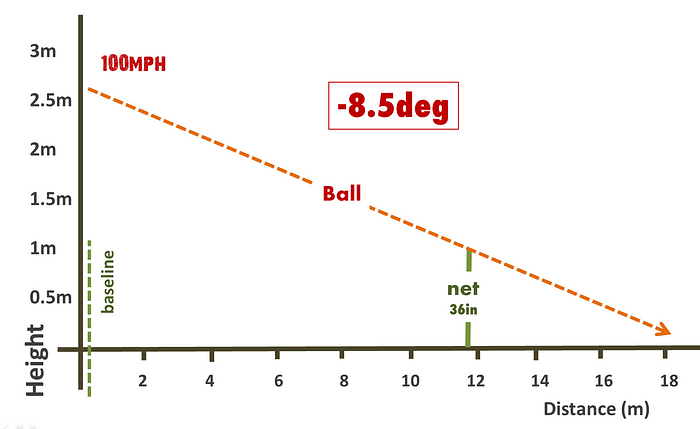
We are clearly forgetting a few physics variables. Any ideas which ones?
● Hint: For a tennis ball to go in, we need to think more like projectiles (eg arrows) in the air.
And now for the 100mph proof.
To generate a better model, we need a combination of trigonometry (triangles) and projectile motion and aerodynamics. OK here is the calculation assuming the ball travels 100mph throughout (ie no drag):
First, you have to work out the average serving height of on the Pro Tour. This is a combination of height, reach and jump. Answer 2.7m
Next work out the distance to the net from the baseline (11.88m) and then on to the service line. Answer 18.28m
Next work out how much the ball falls due to gravity between the baseline and the net at 100mph (44.5m/s). Answer 35cm
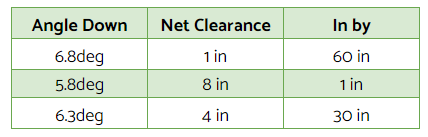
Next work out the max downward angle to *only just* clear the net by lets say 1 inch. Answer 6.8deg
Next work out the minimum downward angle to *only just* get the ball into the service box, let’s say 1 inch. Answer 5.8deg
Here is a draft table of results (assuming constant velocity).
And now for the proof including aero drag.
OK in this case, we will add in drag. So we know the ball begins at 100mph (remember that’s in a diagonal direction, so there is a forward and downward component). AND it slows with a rather rapid deceleration rate of approximately 66mph/s.
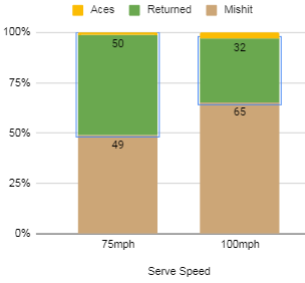
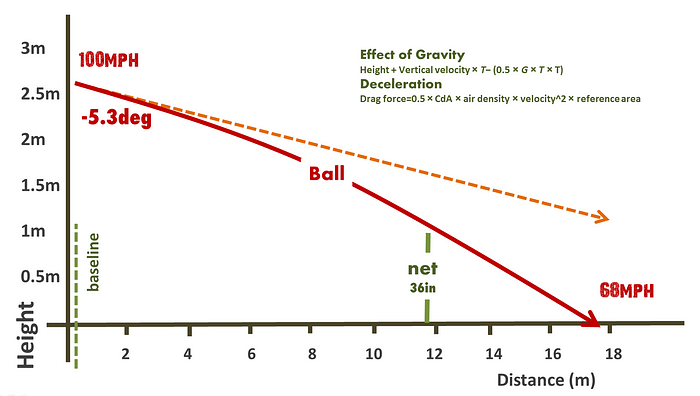
So, a serve will slow from 100mph to around 68mph at the bounce. It actually slows another 10mph on the bounce and hits the opponents racket around 45–55mph (depending on the surface). From this, the average ball speed (before the bounce) is around 84mph (37.6m/s). So recalculating….
Serving height on the Pro Tour. Answer 2.7m
Distance to the net from the baseline (11.88m) and service line. Answer 18.28m
How much the ball falls due to gravity between the baseline and the net at 84mph (37.6m/s). Revised Answer 50cm
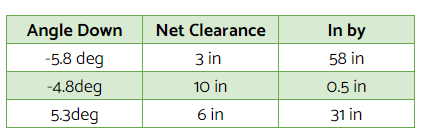
Next work out the max downward angle to *only just* clear the net by let’s say >1 inch. Answer 5.8deg
Next work out the minimum downward angle to *only just* get the ball into the service box, let’s say 1 inch. Answer 6.8deg
Which leaves the optimal service angle of -5.3deg.
Here is a final summary table and figure.
Take Away lessons about the 100mph Serve
So what we have learned is that a 100mph serve is seriously impressive. It crosses the net within 0.3 seconds and hits the ground after 0.5s at a downward angle of -11 degrees. It slows about 50% to the opponents racket (although not so much on a slippery surface!).
● To achieve this serve, you have to serve between minus 5.8deg and minus 4.8deg every time which is only 1 degree of variation!
● It is extremely difficult to get the ball more than 1.5m (60 inch) into service box (without topspin) and maintain 100mph
● It is extremely difficult to get the ball in and serve more than 10 inches above the net (without topspin)
It would be almost impossible to get a 100mph serve in without the benefits of gravity and aerodrag. This is because the clearance of a straight line over the net and into the service box is within one tenth of a degree of -8.5deg. In fact without the ball falling down >1m during its 0.5s flight, it would be ten times harder to get the ball in than it is now. Wow.